Focal Loss for Dense Object Detection
Research Topic
- Category (General): Deep Learning
- Category (Specific): Computer Vision
Paper summary
- Propose a new loss function tackling the extreme class imbalance problem encountered in object detections.
- Reshaping Cross Entropy Loss Function such that it down-weights the loss assigned to well-classified examples.
- Understand if one-stage de-tectors can match or surpass the accuracy of two-stage detectors while running at similar or faster speeds.
- Introduce the RetinaNet to evaluate the effectiveness of the loss, but since the author stated: “Our simple detector achieves top results not based on innovations in network design but due to our novel loss.”, I’m gonna skip the RetinaNet in this recap.
Explain Like I’m 5 (ELI5) 👶👶👶
- Basically it is Balanced Cross Entropy Loss Function but with a tunable modulating factor such that it controls the weight loss of easy/hard samples.
Issues addressed by the paper
- Current state-of-the-art object detectors are based on a two-stage, proposal-driven mechanism, which consistently achieves top accuracy on the challenging COCO benchmark.
- Could a simple one-stage detector achieve similar accuracy?
- Recent work on one-stage detectors yield faster detectors with accuracy within 10-40% relative to state-of-the-art two-stage methods, but takes also a lot of time.
- Class imbalance is addressed in R-CNN-like (one-stage) detectors by a two-stage cascade and sampling heuristics.
- An one-stage detector must process a much larger set of candidate object locations regularly sampled across an image, which makes the model inefficient as the training procedure is still dominated by easily classified background examples.
- Balanced CE loss function: while \(\alpha\) balances the importance of positive/negative examples, it does not differentiate between easy/hard examples.
Approach/Method
- Present a one-stage object detector (RetinaNet) that, for the first time (by the time of publish), matches the state-of-the-art COCO AP.
- To achieve this result:
- Identify class imbalance during training as the main obstacle impeding one-stage detector from achieving state-of-the-art accuracy,
- Propose a new loss function that eliminates this barrier.
- Focal Loss:
- Dynamically scaled cross entropy loss.
- Automatically down-weight the contribution of easy examples (inliers) during training and rapidly focus the model on hard examples.
- Focal loss performs the opposite role of a robust loss (e.g: Huber Loss): it focuses training on a sparse set of hard examples.
- They first defined the probability function like this:
- Using this definition, we can define CE loss func like this: \(CE(p,y) = CE(p_t) = -log(p_t)\) for comparision.
- Balanced Focal Loss’s definition:
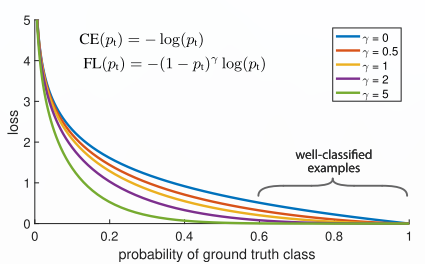
- When an example is misclassified and \(p_t\) is small, the modulating factor is near 1 and the loss is unaffected. As \(p_t \to 1\), the factor goes to 0 and the loss for well-classified is down-weighted.
- The focusing parameter \(\gamma\) smoothly adjusts the rate at which easy examples are down-weighted.
- When \(\gamma = 0\), focal loss is equivalent to cross entropy loss, as \(\gamma\) is increased the effect of the modulating factor is likewise increased.
Best practice
- \(\gamma = 2\) works well in practice.
- The benefit of changing \(\gamma\) is much larger, and indeed the best \(\alpha\)’s ranged in just [.25,.75].
- In general \(\alpha\) should be decreased slightly as \(\gamma\) is increased.
Hidden gems💎💎💎
- In practice \(\alpha\) (of Balanced CE) may be set by inverse class frequency or treated as a hyperparameter to set by cross validation.
- One notable property of CE loss, which can be easily seen in the upper plot, is that even examples that are easily classified incur a loss with non-trivial magnitude. When summed over a large number of easy examples, these small loss values can overwhelm the rare class.
- Two-stage detectors are often trained with the CE loss without use of \(\alpha\)-balancing, but address class imbalance through two mechanisms: (1) a two-stage cascade and (2) biased minibatch sampling.
- Feature Pyramid Network augments a standard convolutional network with a top-down pathway and lateral connections so the network efficiently constructs a rich, multi-scale feature pyramid from a single resolution input image.
- Larger backbone networks yield higher accuracy, but also slower inference speeds, likewise for input image scale.
Confusing aspects of the paper
- The different between easy and hard sample?
- The difference between the two is not obvious from the paper.
- IMO, easy samples means that the probability \(p_t\) is close to the class (1 for positive, 0 for negative), vice versa for the hard samples.
- Why \(\alpha\)-balancing of CE doesn’t differentiate between easy/ hard examples?
- This issue is also not verified in the paper.
- IMO, \(\alpha\) is only used to address the imbalanced class problem (since its value also tuned for the same reason), Focal Loss adds the modular factor which directly affected by the probability that the model suggested and adjust the loss.
Results
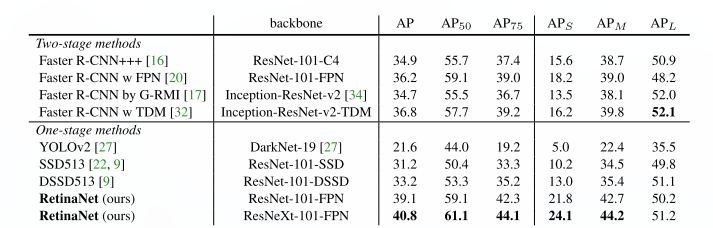
- The model achieves top results, outperforming both one-stage and two-stage models.
Conclusions
The author’s conclusions
- Focal loss applies a modulating term to the cross entropy loss in order to focus learning on hard negative examples.
- The approach is simple and highly effective.
Rating

Paper implementation
class FocalLoss(nn.Module):
def __init__(self, n_class, alpha=None, gamma=2, reduction='mean'):
super(FocalLoss, self).__init__()
if alpha is None:
self.alpha = Variable(torch.ones(n_class, 1))
else:
self.alpha = alpha if isinstance(alpha, Variable) else Variable(alpha)
self.gamma = gamma
self.n_class = n_class
self.reduction = reduction
def forward(self, inputs, targets):
device = inputs.device
bs = inputs.size(0)
n_channel = inputs.size(1)
probs = F.softmax(inputs)
class_mask = inputs.data.new(bs, n_channel).fill_(0)
class_mask = Variable(class_mask)
ys = targets.view(-1, 1)
# onehot encoding
class_mask.scatter_(1, ys.data, 1.)
if inputs.is_cuda and not self.alpha.is_cuda:
self.alpha = self.alpha.to(device)
alphas = self.alpha[ys.data.view(-1)]
probs = (probs*class_mask).sum(1).view(-1,1)
log_p = probs.log()
batch_loss = -alphas*(torch.pow((1-probs), self.gamma))*log_p
if self.reduction == "mean":
loss = batch_loss.mean()
else:
loss = batch_loss.sum()
return loss
Cited references and used images from:
Papers needed to be conquered next 👏👏👏
- SIMCLR maybe?