Paper recap: CutMix

CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features

Yun, Sangdoo Han, Dongyoon Chun, Sanghyuk Oh, Seong Joon Choe, Junsuk Yoo, Youngjoon

Research Topic

• Category (General): Deep Learning
• Category (Specific): Data Augmentation

Paper summary

• Introduce a new data augmentation method: CutMix, which helps:
  • Generates new samples by cutting and pasting patches within mini-batches, leading to performance boosts in many computer vision tasks.
  • Improves the model robustness against input corruptions
  • Performs better when facing out-of-distribution detection problems.

Explain Like I’m 5 (ELI5) 👶👶👶

Issues addressed by the paper

• Regional cutout may remove informative pixels, in addition to it, these techniques also add noises by replace those cut pixels with black area.
• How can we maximally utilize the deleted regions, while taking advantage of better generalization and localization using regional dropout?
• While certainly improving classification performance, Mixup samples tend to be unnatural.
• Synthesizing training data guides also improves model performance, but introduces costly computations.
• Recently, methods adding noises to the internal features of CNNs or adding extra path to the architecture have been proposed to enhance image classification performance.
• Cutmix has properties such that can compensate all of those mentioned above.

Approach/Method

• Core idea: We have 2 pictures, choose a region (apply to both pictures) in the image that is proportional to the image’s ratio, then swap those regions, leads to a new sample.

    new_image = MASK * image_1 + (1-MASK) * image_2
    new_label = lambda * label_1 + (1-lambda) * label_2
  

• lambda is sampled from symmetric Beta distribution (having same \(\alpha\) and \(\beta\) value), which looks like the following image. This distribution makes sure that the new image will most of the time be close only to the first or the second picture. Only sometimes both images have the same intensity (of course if in a case of multicategorical, other label will be 0).

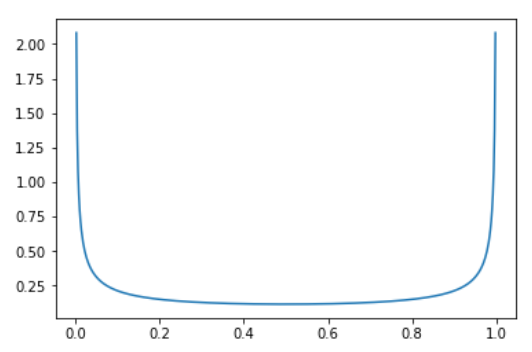
• MASK has the same WxH like the original image, having full 0s in the region that is gonna be cutout (let’s call it B) and full 1s in the leftover pixels.
• B is a bounding box, having coordinates defined as \(B = (r_x, r_y, r_w, r_h)\) indicating the cropping regions.

\[r_x \sim Unif(0,W); \: r_w = W \sqrt{1 - \lambda} \\ r_y \sim Unif(0,H); \: r_h = H \sqrt{1 - \lambda}\]

• Having these coordinates defined like this would make the cropped area ratio equals to \(1 - \lambda\).

Result

• CutMix overcomes the problem of both Mixup (its samples tend to be unnatural) and regional cutout (removes informative pixels) by replacing the image region with a patch from another training image.
• CutMix incurs only negligible additional cost for training.
• Cutout successfully lets a model focus on less discriminative parts of the object.

• Outperforms other SOTAs using data augmentation during the time of publish.

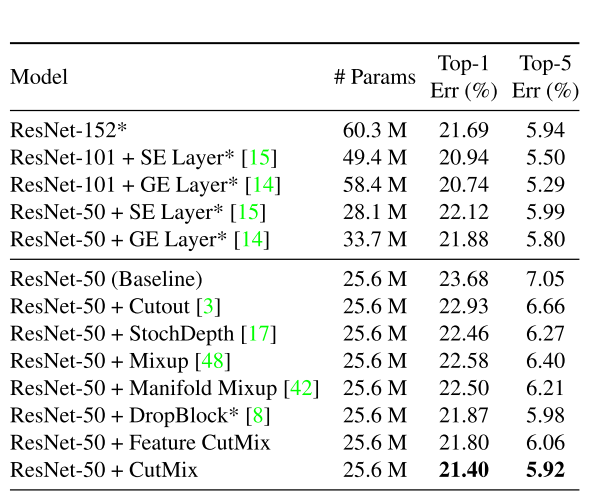
Best practice

• \(\alpha = 1\) usually performs well.
• Cutout, Mixup, and CutMix require a greater number of training epochs till convergence.
• CutMix achieves the best performance when it is applied on the input images rather than hidden features.
• A new state-of-the-art performance 13.81% (in CIFAR-100) by combining CutMix and ShakeDrop, a regularization that adds noise on intermediate features.

Hidden gems💎💎💎

• Label-smoothing is good when apply together with data augmentation such as Cutout, Mixup, Dropblock.
• Mixup, Manifold Mixup achieve higher accuracies when Cutout is applied on input images.

Conclusions

Rating

Paper implementation

• Using Pytorch Lightning Callback system, inspired by fastai implementation.

    class MixLoss(nn.Module):
        def __init__(self, old_lf, mixup_cb):
            super().__init__()
            self.old_lf = old_lf
            self.mixup_cb = mixup_cb
  
        def forward(self, pred, yb):
            if self.mixup_cb.pl_module.testing: return self.old_lf(pred, yb)
            with NoneReduce(self.old_lf) as lf:
                self.mixup_cb.yb_1 = self.mixup_cb.yb_1.to(pred.device)
                self.mixup_cb.lam = self.mixup_cb.lam.to(pred.device)
                loss = torch.lerp(lf(pred, self.mixup_cb.yb_1), lf(pred,yb), self.mixup_cb.lam)
            return reduce_loss(loss, getattr(self.old_lf, 'reduction', 'mean'))
  
    # Cell
    class CutmixDict(Callback):
        def __init__(self, alpha=1.):
            super().__init__()
            self.distrib = Beta(tensor(alpha), tensor(alpha))
  
        def on_train_start(self, trainer, pl_module):
            assert hasattr(pl_module, 'loss_func'), 'Your LightningModule should have loss_func attribute as your loss function.'
            self.old_lf = pl_module.loss_func
            self.loss_fnc = MixLoss(self.old_lf, self)
            pl_module.loss_func = self.loss_fnc
            self.pl_module = pl_module
  
        def _cutmix(self, batch, logger, log_image=False, pre_fix='train'):
            xb, yb = batch["img"], batch["label"]
            bs = yb.size(0)
            W, H = xb.size(3), xb.size(2)
  
            lam = self.distrib.sample((1,)).squeeze()
            lam = torch.stack([lam, 1-lam])
            self.lam = lam.max()
  
            # Permute the batch
            shuffle = torch.randperm(bs)
            xb_1, self.yb_1 = xb[shuffle], yb[shuffle]
  
            x1, y1, x2, y2 = self.rand_bbox(W, H, self.lam)
            xb[:, :, x1:x2, y1:y2] = xb_1[:, :, x1:x2, y1:y2]
            self.lam = (1 - ((x2-x1) * (y2-y1)) / float(W*H))
  
            if log_image:
                grid = torchvision.utils.make_grid(xb)
                logger.experiment.add_image(pre_fix + '_cutmix', grid)
                grid_g = torchvision.utils.make_grid(xb_1)
                logger.experiment.add_image(pre_fix + '_cut_from', grid_g)
                dif = abs(xb - xb_1)
                grid_d = torchvision.utils.make_grid(dif)
                logger.experiment.add_image(pre_fix + '_dif', grid_d)
            return xb
  
        def on_train_batch_start(self, trainer, pl_module, batch, batch_idx, dataloader_idx):
            x = self._cutmix(batch, trainer.logger)
            batch["img"] = x
  
        def on_validation_start(self, trainer, pl_module):
            pl_module.loss_func = self.old_lf
  
        def on_validation_end(self, trainer, pl_module):
            pl_module.loss_func = self.loss_fnc
  
        def on_fit_end(self, trainer, pl_module):
            pl_module.loss_func = self.old_lf
  
        def rand_bbox(self, W, H, lam):
            cut_rat = torch.sqrt(1. - lam)
            cut_w = (W * cut_rat).type(torch.long)
            cut_h = (H * cut_rat).type(torch.long)
            # uniform
            cx = torch.randint(0, W, (1,))
            cy = torch.randint(0, H, (1,))
            x1 = torch.clamp(cx - cut_w // 2, 0, W)
            y1 = torch.clamp(cy - cut_h // 2, 0, H)
            x2 = torch.clamp(cx + cut_w // 2, 0, W)
            y2 = torch.clamp(cy + cut_h // 2, 0, H)
            return x1, y1, x2, y2
  

Papers needs to conquer next 👏👏👏

• Any recommendation?