A disciplined approach to neural network hyper-parameters: Part 1
Research Topic
- Category (General): Deep Learning.
- Category (Specific): Hyperparameters Tuning.
Paper summary
- Introduce techniques to set some essential hyper-parameters such as: learning rate, batch size, momentum, weight decay.
- How to examine training/ test loss curve for clues of underfitting, overfitting.
- Introduce a new method of cyclical learning rate: 1cycle policy.
- Discuss about cyclical momentum, cyclical weight decay.
- Produce multiples examples to show the importance of balanced regularization for each dataset/ architecture.
Explain Like I’m 5 (ELI5) 👶👶👶
- Not necessary since this paper mostly tackle best pratices while working on projects.
Issues addressed by the paper
- Grid-search is computationally expensive and time consumming. But a good choice of hyper-parameters is vital for a model to perform well, so how to do grid-search efficiently?
- Underfitting/ overfitting trade-off.
- Learning rate:
- Too small: overfitting can occur.
- Too large: can have regularize but will diverge.
- Batch size:
- Suggest that when we comparing batch size, neither maintaining constant #epochs (train the same #epochs for each batch size) nor constant #iterations (train the same #iterations/epoch each batch size) is appropriate:
- constant #epochs:
- Computationally efficient, but penalized more since we see a big proportion of samples each time.
- constant #iterations:
- Overfit will occur.
- constant #epochs:
- Batch size directly affect computational time.
- Suggest that when we comparing batch size, neither maintaining constant #epochs (train the same #epochs for each batch size) nor constant #iterations (train the same #iterations/epoch each batch size) is appropriate:
- Momentum:
- Momentum and learning rate are closely related and its optimal values are dependent on each other.
- Momentum’s effect on updating the weights is of the same magnitude as the learning rate (used SGD with momentum equation to verify).
- Weight decay:
- Weight decay is one form of regularization and it plays an important role in training so its value needs to be set properly.
Approach/Method
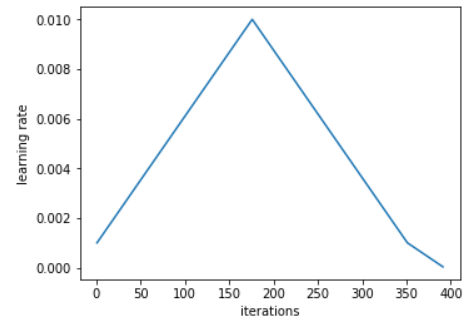
- 1cycle policy:
- Instead of cyclical learning rate using
triangularas the previous post, the author suggest to:- Train all epochs in more than one cycle just a small proportion.
- In the remaining iterations, the learning rate will decline from
base_lrto several orders of magnitude less.
- Experiments show that this policy allows the accuracy to plateau before the training ends.
- Instead of cyclical learning rate using
- The author show these 6 remarks after multiple researchs and experiments:
- The test/validation loss is a good indicator of the network’s convergence and should be examined for clues.
- Look at the loss curve and also plot generalization error curve (
valid_loss - train_loss), one can determine whether the architechture has the capacity to overfit or has too small learning rate (which also leads to overfit)
- Look at the loss curve and also plot generalization error curve (
- Achieving the horizontal part of the test loss is the goal of hyperparameter tuning.
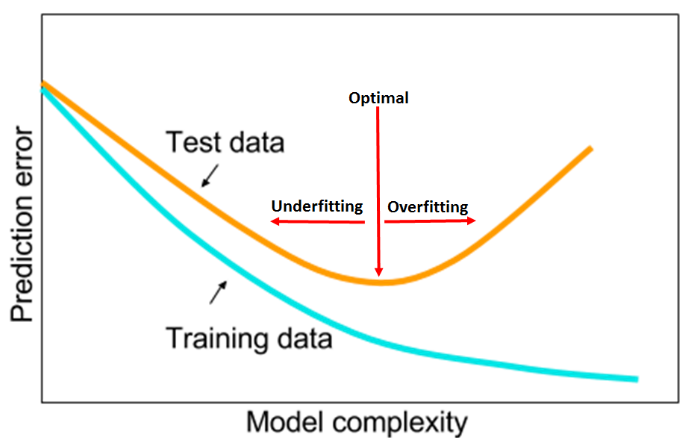
- The horizontal part is the red line.
- The amount of regularization must be balanced for each dataset and architecture.
- The practitioner’s goal is obtaining the highest performance while minimizing the needed computational time.
- Optimal momentum value(s) will improve network training.
- Since the amount of regularization must be balanced for each dataset and architecture, the value of weight decay is a key knob to turn for tuning regularization against the regularization from an increasing learning rate.
- The test/validation loss is a good indicator of the network’s convergence and should be examined for clues.
Best practices
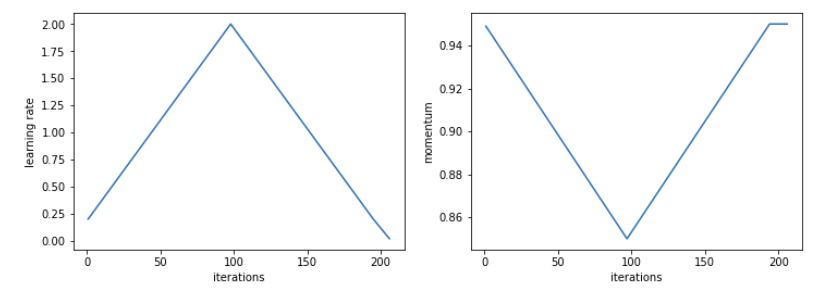
- Learning rate:
- Use learning rate range test to find the minimum and maximum learning rate boundaries:
- Maximum learning rate bound: the maximum value that the model can still converge
- Minumum learning rate bound:
- \(\frac{1}{3};\frac{1}{4}\) of max bound.
- \(\frac{1}{10};\frac{1}{20}\) of max bound if using 1cycle.
- Use 1cycle policy to achive super-convergence (reachs global optima with iterations much less than regulars).
- Other regularization methods must be reduced to compensate for the regularization effects of large learning rates.
- Use learning rate range test to find the minimum and maximum learning rate boundaries:
- Batch size:
- Small batch sizes add regularization, large batch sizes add less; utilize this while balancing the proper amount of regularization.
- Often better to use a larger batch size so a larger learning rate can be used (leads to using a larger batch size when using the 1cycle learning rate schedule).
- Momentum:
- Short runs with momentum values of 0.99, 0.97, 0.95, and 0.9 will quickly show the best value for momentum.
- If use 1cycle policy, should use cyclical momentum starting at maximum momentum value and decreasing to a value of 0.8 or 0.85 (performance is almost independent of the minimum momentum value).
- Decreasing cyclical momentum when the learning rate increases provides an equivalent result to the best constant momentum value.
- Using cyclical momentum along with the LR range test stabilizes the convergence when using large learning rate values more than a constant momentum does.
- Weight decay:
- Should be a constant value.
- Should use grid search to find a proper value; validation loss early in the training is sufficient for determining a good value.
- Another option as a grid search for weight decay is to make a single run at a middle value for weight decay and save a snapshot after the loss plateaus. Use this snapshot to restart runs, each with a different value of WD. This can save time in searching for the best weight decay.
- A complex dataset requires less regularization so test smaller weight decay values, such as \(10^{−4}, 10^{−5}, 10^{−6}, 0\)
- A shallow architecture requires more regularization so test larger weight decay values, such as \(10^{−2}, 10^{−3}, 10^{−4}\).
- The optimal weight decay is different if you search with a constant learning rate versus using a learning rate range.
Hidden gems💎💎💎
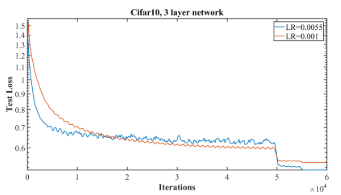
- Test loss decreases more rapidly during the initial iterations and is then horizontal is an early positive clue indicating that the model will produce a better final accuracy. (Blue curve)
- Learning rates that are too small can exhibit some overfitting behavior.
- There is a maximum speed the learning rate can increase without the training becoming unstable.
- The very large learning rates provided the twin benefits of regularization that prevented overfitting and faster training of the network.
- Set momentum as large as possible without causing instabilities during training.
- Momentum range test is not useful for finding an optimal momentum, you should use grid search.
- Decreasing the momentum while the learning rate increases provides three benefits (by experiments):
- a lower minimum test loss.
- faster initial convergence.
- greater convergence stability over a larger range of learning rates.
- Large momentum helps escape saddle points but can hurt the final convergence, implying that momentum should be reduced at the end of training.
- A good procedure is to test momentum values in the range of 0.9 to 0.99.
- All the general ideas can apply to shallow or deep networks, although the details (i.e., specific values for momentum) varied.
Results
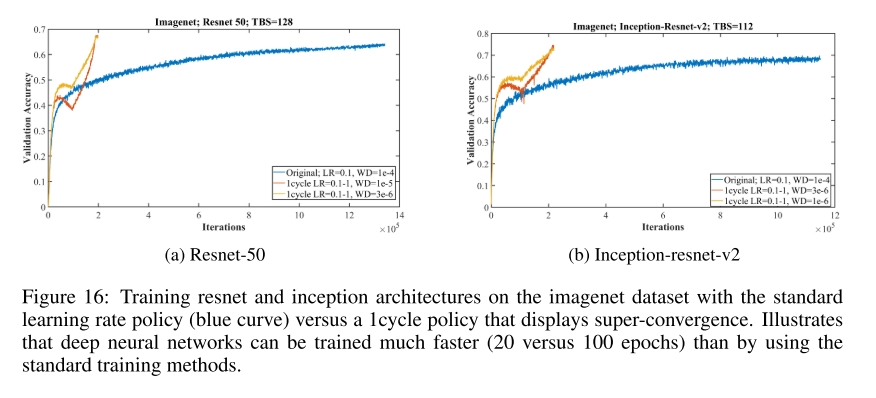
- As the experiment shown, if one can find optimal values for these hyper-parameters, the model would achieve super-convergence, which saves computational cost and time.
Limitations
- These disciplines are not proved but mostly achieved by experiments. So we can only use this as a guide and apply it to our projects.
Confusing aspects of the paper
- Very straightforward, confusing-free.
Conclusions
Rating
Would read again.
My conclusion
- Good workflow to deal with hyper-parameters.
- Can be use as a reference when start a new projects.
Paper implementation

Cited references and used images from:
- Lesli N.Smith, 2018
- https://sgugger.github.io/the-1cycle-policy.html
- https://github.com/asvcode/1_cycle